Il 20 marzo il matematico americano/canadese Robert Langlands ha vinto il Premio Abel, assegnatogli per coronare una vita di traguardi e scoperte nel campo della matematica. Le sue ricerche hanno dimostrato come sia possibile mettere insieme concetti provenienti dalla geometria, dall’algebra e dall’analisi, sfruttando il comune legame con i numeri primi. E per questo, quando a maggio il re norvegese consegnerà il premio a Langlands non farà che onorare l’esempio più recente in 2.300 anni di sforzi volti a comprendere i numeri primi, certamente il più antico e vasto set di dati mai studiato dalla matematica.
Come matematico che ha dedicato la propria ricerca a questo “Langlands program”, io sono affascinato dalla storia dei numeri primi e dalle scoperte più recenti che iniziano a rivelare alcuni dei loro segreti. Perché dunque affascinano i matematici da millenni?
La caccia ai numeri primi
Per studiare i numeri primi i matematici non fanno altro che passare numeri interi attraverso diversi “setacci virtuali”, fino a che non quello che rimane non sono solamente numeri primi. Nel diciannovesimo secolo questo processo di setacciatura ha prodotto tavole contenenti milioni di numeri primi. Mentre oggi permette ai computer di trovarne miliardi in meno di un secondo. Ma l’idea di base non è mai cambiata nel corso di più di duemila anni.
“Un numero primo è quello che viene misurato unicamente dall’Unità”, scriveva Euclide nel 300 a.C. Questo vuol dire che un numero primo non può essere diviso senza resto per nessun numero inferiore a sé stesso, a parte l’uno. Per convenzione, i matematici non considerano invece il numero uno come primo.
E se Euclide ha dimostrato l’infinità dei numeri primi – il fatto che ne esiste un numero infinito – la storia suggerisce che sia stato invece Eratostene a fornirci il setaccio con cui possiamo identificarli.
Ecco come funziona. Per prima cosa, bisogna eliminare i multipli di 2, poi di 3, poi di 5 e di 7 – i primi quattro numeri primi. Facendolo per tutti i numeri da 2 a 100 rimarranno solamente numeri primi.
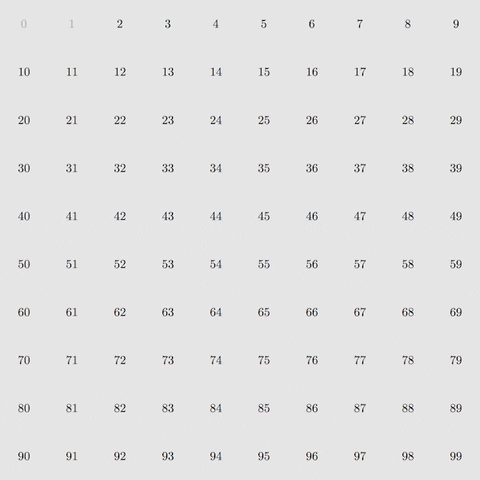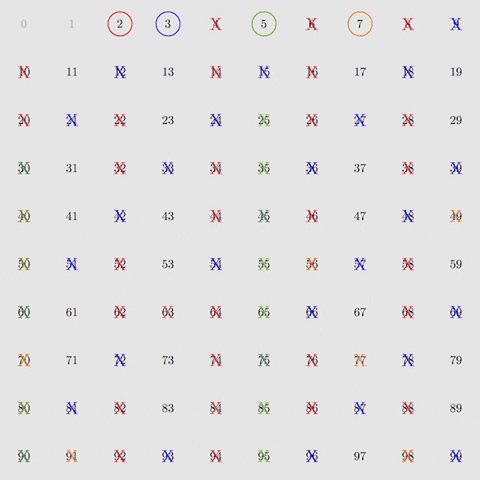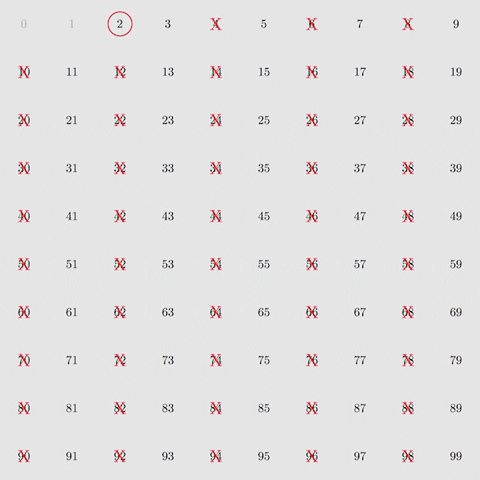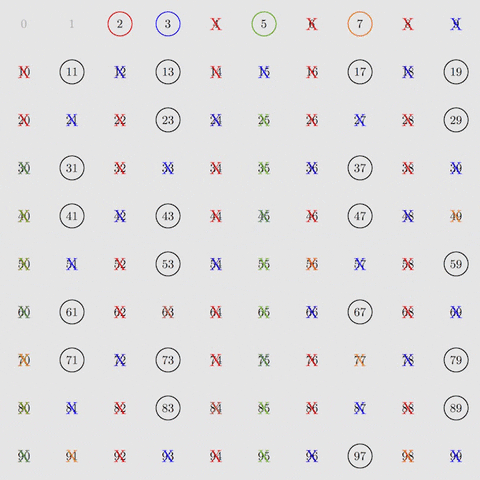Eliminando i multipli di 2, 3, 5 e 7 rimangono solo i numeri primi tra 1 e 100. Courtesy of M.H. Weissman.
Con otto passaggi simili è possibile isolare tutti i numeri primi fino a 400. Con 168 passaggi si può arrivare fino al milione. È questo il potere del setaccio di Eratostene.
Tavole e tabelle
Uno dei primi a tabulare i numeri primi è stato John Pell, un matematico inglese che ha dedicato larga parte del suo lavoro alla creazione di tabelle di numeri utili. A spingerlo in questa sua impresa era da un lato il desiderio di risolvere alcuni antichi problemi aritmetici di Diofanto, dall’altro la missione personale di voler dare un’organizzazione alle verità matematiche. Grazie ai suoi sforzi, già all’inizio del 1700 i numeri primi fino a 100.000 erano ampiamente noti. E arrivati al 1800 diversi progetti indipendenti avevano tabulato i numeri primi fino ad un milione.
Per automatizzare questi passaggi di setaccio, piuttosto noiosi, il matematico tedesco Carl Friedrich Hindenburg sviluppò quindi una serie di slider aggiustabili, per identificare in un colpo solo tutti i multipli presenti su una pagina. Un simile approccio, poco tecnologico ma molto efficace, fu quello di fare ricorso a degli stencil per identificare i multipli. Per la metà del 1800, il matematico Jakob Kulik si era imbarcato nell’ambizioso progetto di identificare tutti i numeri primi fino a 100 milioni.
Questi “big data” del 1800 sarebbero probabilmente stati utilizzati semplicemente come tabelle di riferimento, se Carl Friedrich Gauss non avesse deciso di iniziare ad analizzare i numeri primi di per sé stessi. Armato di una lista dei numeri primi fino a 3 milioni, Gauss iniziò a contarli a gruppi di mille unità. Calcolò i numeri primi fino a 1.000, poi quelli compresi tra 1.000 e 2.000, quindi quelli tra 2.000 e 3.000, e così via.
Gauss scoprì così che con il crescere delle cifre i numeri primi divenivano sempre meno frequenti, seguendo una legge logaritmica inversa. La Legge di Gauss non ci dice esattamente quanti numeri primi esistono, ma ci fornisce una stima piuttosto accurata. Per fare un esempio, la sua legge prevede che esistano 72 numeri primi compresi tra 1.000.000 e 1.001.000. Il numero esatto è 75 numeri primi, che vuol dire una percentuale di errore intorno al 4%.
Ad un secolo dalle prime indagini di Gauss, la sua legge è stata dimostrata con il “teorema del numeri primi”. La percentuale di errore si avvicina progressivamente allo zero al crescere dei numeri analizzati. Anche l’ipotesi di Riemann, che oggi è un problema matematico da un milione di dollari, descrive quanto sia accurata la legge di Gauss.
Il Teorema dei numeri primi e l’Ipotesi di Riemann ricevono tutte le attenzioni e il denaro, ma entrambe sono la conseguenza di lavori precedenti, e meno accattivanti, di analisi dei dati.
I misteri moderni dei numeri primi
Oggi i nostri set di dati arrivano dai computer piuttosto che da stancil tagliati a mano, ma i matematici continuano a trovare sempre nuovi pattern e regolarità nei numeri primi. A parte 2 e 5, tutti i numeri primi terminano con un 1, 3, 7 o 9. Nel 1800 è stato dimostrato che tutte queste possibili cifre finali sono ugualmente frequenti. In altre parole, se osserviamo i numeri primi fino a un milione circa il 25% terminerà con un 1, il 25% con un 3, il 25% con un 7 e il 25% con un 9.
(Grafico sul numero terminale dei numeri primi qui).
Qualche anno fa gli esperti di teoria dei numeri di Stanford Robert Lemke Oliver e Kannan Soundararajan furono colti di sorpresa da una stranezza nelle cifre finali dei numeri primi. Un esperimento si era concentrato sull’ultima cifra di un numero primo, in connessione con l’ultima cifra di quello precedente e di quello seguente. Per fare un esempio, il numero primo che segue 23 è il 29: le cifre finali sono 3 e 9. Questa seguenza, prima tre e poi nove, è più comune tra le ultime cifre dei numeri primi, rispetto ad esempio a un 3 e poi un 7?
Gli esperti di teoria dei numeri si aspettavano di trovare una certa variabilità, ma quello che hanno scoperto superava di gran lunga le loro aspettative. I numeri primi sono separati da differenti gap; ad esempio 23 è a sei numeri di distanza da 29. Ma la sequenza di numeri primi che terminano con il numero 3 e poi con il numero 9, come 23 e 29, è molto più comune di quella di numeri primi che terminano con un 7 e poi con un 3, nonostante entrambe le sequenze siano separate da un gap di 6 numeri.
In breve tempo i matematici hanno trovato una spiegazione plausibile. Ma quando parliamo dello studio dei numeri primi che si succedono, i matematici si devono limitare per lo più all’analisi dei dati e alla persuasione. Le prove – il golden standard dei matematici per spiegare perché un qualcosa è vero – sembrano ancora a decenni di distanza.
L’articolo è stato pubblicato in inglese su The Conversation. Traduzione a cura della redazione di Galileo.
