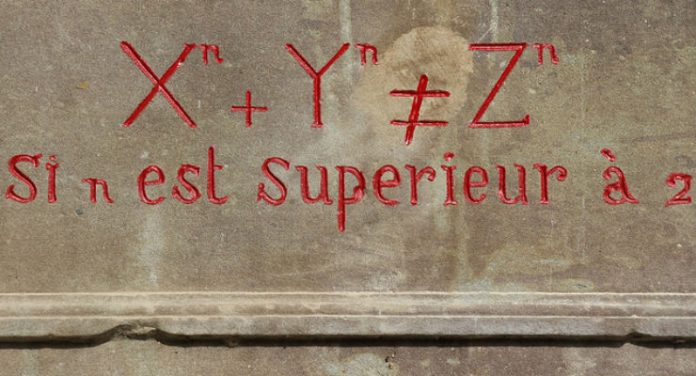A oltre 20 anni dalla sua più grande scoperta, Sir Andrew Wiles è stato nominato vincitore dell’Abel prize 2016. Il premio, vinto lo scorso anno da Louis Nirenberg e John Nash (morto quattro giorni dopo aver ricevuto il premio in un incidente automobilistico), viene assegnato ogni anno dal governo norvegese ai più importanti matematici del pianeta, ed è considerato da molti l’equivalente del premio Nobel per la matematica, insieme alla medaglia Fields. Wiles, oggi professore di matematica dell’università di Oxford, ha ricevuto il premio, e i circa 600mila euro che porta con sé, per la sua dimostrazione di uno dei più famosi problemi della matematica: il teorema di Fermat.
Per chi non lo ricordasse (a rendere celebre contribuì un libro del giornalista inglese Simon Singh, L’ultimo teorema di Fermat), il teorema, che il grande matematico francese Pierre Fermat formulò nel 1637, afferma che l’equazione an + bn = cn non ha soluzioni intere positive, se n è superiore a due.
Si tratta, come è evidente, di un problema piuttosto semplice da comprendere, ma la cui dimostrazione (che Fermat assicurò di possedere, ma non rese mai pubblica prima della morte) è stata inseguita dal mondo della matematica per oltre tre secoli.
Proprio la semplicità del problema contribuì a catturare l’attenzione di Wiles, che vi si imbatté all’età di 10 anni, e continuò a studiarlo per il resto della vita. Fino ad imbarcarsi, una volta diventato professore di matematica a Princeton, in una solitaria ricerca durata sette anni, da cui emerse nel 1993 con la prima dimostrazione mai trovata per il teorema. Qui la vicenda si fece ancor più romanzesca, perché a soli due mesi dalla pubblicazione della dimostrazione venne trovato un errore fondamentale nella formulazione di Wiles, che costrinse il matematico a tornare a lavoro. Con il contributo del suo primo studente, Richard Taylor, Wiles lavorò per più di un anno sulle formule, fino a trovare una soluzione corretta, che venne pubblicata nel 1995.
La dimostrazione trovata da Wiles combina tre campi estremamente complessi della matematica, utilizzando strumenti di geometria algebrica, della teoria di Galois, della teoria delle curve ellittiche e delle forme modulari, un risultato che in molti reputano più importante del teorema di Fermat in sé. Lo stesso comitato del premio Abel riconosce la conquista di Wiles, affermando che il premio è stato assegnato per “La sua incredibile dimostrazione dell’Ultimo teorema di Fermat attraverso la congettura di modularità delle curve ellittiche semistabili, aprendo una nuova era per la teoria dei numeri”.
Dopo il successo e l’esposizione mediatica ricevute al momento della scoperta, Wiles, che raggiunto da Nature ha assicurato di essere “assolutamente sorpreso” dalla notizia del premio, ha continuato a lavorare ad altri problemi insoluti della matematica. Attualmente si starebbe dedicando alla Congettura di Birch e Swinnerton-Dyer, uno dei sette problemi del millennio secondo il Clay Mathematics Institute di Oxford.
Via: Wired.it
Credits immagine: Renaud Camus/Flickr CC